本章学习内容
- 使用随机数的密码技术
- 随机数的性质
- 伪随机数生成器
- 具体的伪随机数生成器
- 对伪随机数生成器的攻击
使用随机数的密码技术
随机数是干什么用的
随机数在密码技术中十分重要,下面场景会用到随机数:
- 生成秘钥
- 生成密钥对
- 生成初始化向量
- 生成nonce
- 生成盐
伪随机数生成器需要让攻击者无法看穿。
随机数的性质
随机数的性质有以下三类:
- 随机性——不存在统计学偏差,完全杂乱的数列
- 不可预测性——不能从过去的数列推测出下一个数列
- 不可重现性——除非将数列本身保存下来,否则不能重现相同的数列
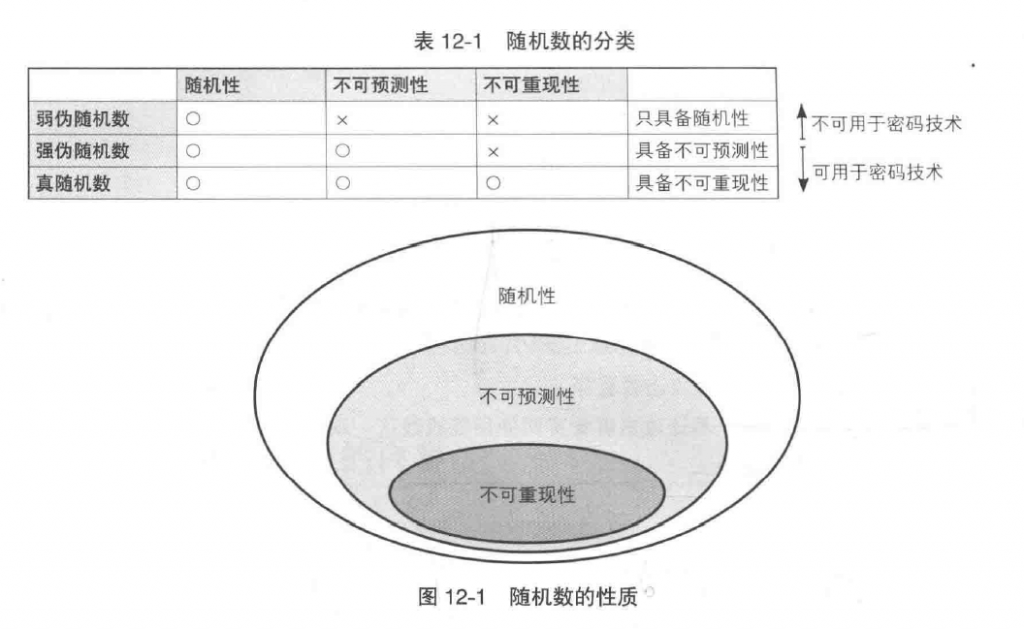
随机性
杂乱无章并不代表不会看穿,所以只能成为弱伪随机数。
不可预测性
攻击者在知道过去生成的伪随机数的前提下依旧无法预测出下一个生成出来的伪随机数。
不可预测性是通过使用其他的密码技术来实现的,例如可以通过单项散列函数的单项性和密码的机密性保证伪随机数的不可预测性。
具备不可预测性的伪随机数称为强伪随机数
不可重现性
不可重现性是无法重现某一个随机数列完全相同的性质。要生成具备不可重现性的随机数列,需要从不可重现的物理现象中获取信息。
具备不可重现性的随机数称为真随机数。
伪随机数生成器
伪随机数生成器的结构
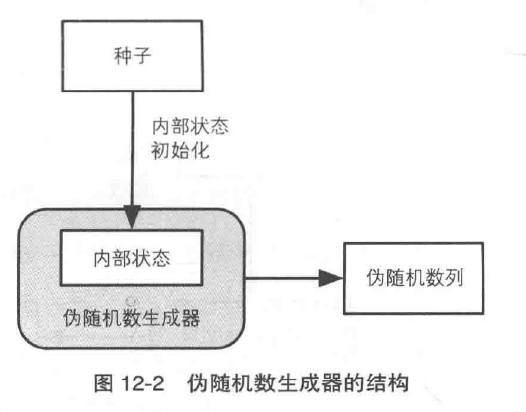
伪随机数生成器的内部状态
伪随机数的内部状态是伪随机数内部管理的内存中的数值。内部状态决定了生成的下一个伪随机数。所以内部状态不能被攻击者知道。
伪随机数生成器的种子
为了生成伪随机数,伪随机数生成器需要被称为种子的信息。
密码的秘钥与伪随机数种子的对比:
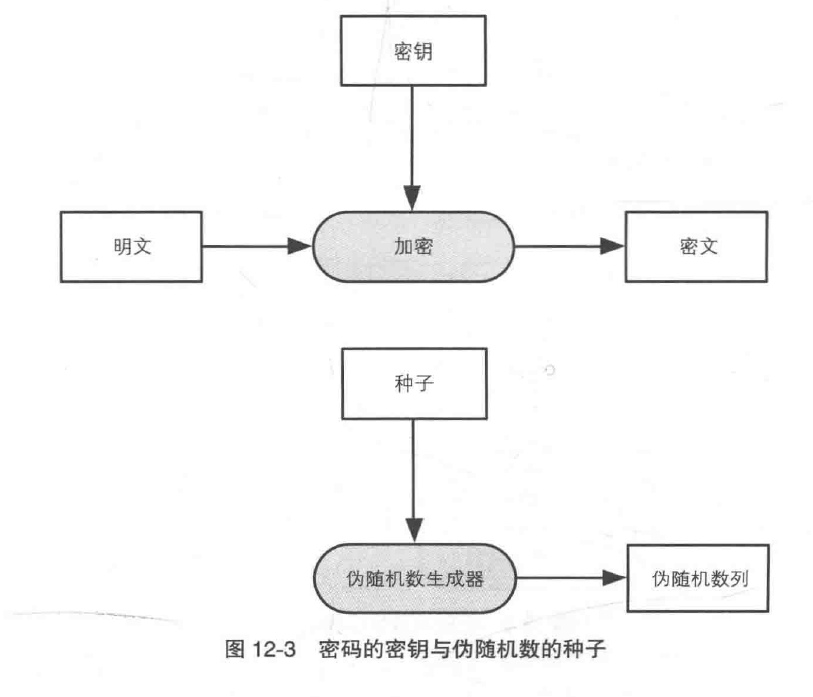
具体的伪随机数生成器
- 杂乱的方法
- 线性同余法
- 单项散列函数法
- 密码法
- ANSI X9.17
杂乱的方法
如果自己使用杂乱的方法来生成伪随机数往往只有很短的周期,安全性很低。
线性同余法
第一个随机数R0 = (A x 种子 + C) mod M
借接下来我们用相同的公式计算下一个伪随机数
R1 = (A x R0 + C)mod M
以此类推。
线性同余法就是讲当前的伪随机数值乘以A再加上C,然后将除以M得到的余数作为下一个伪随机数。
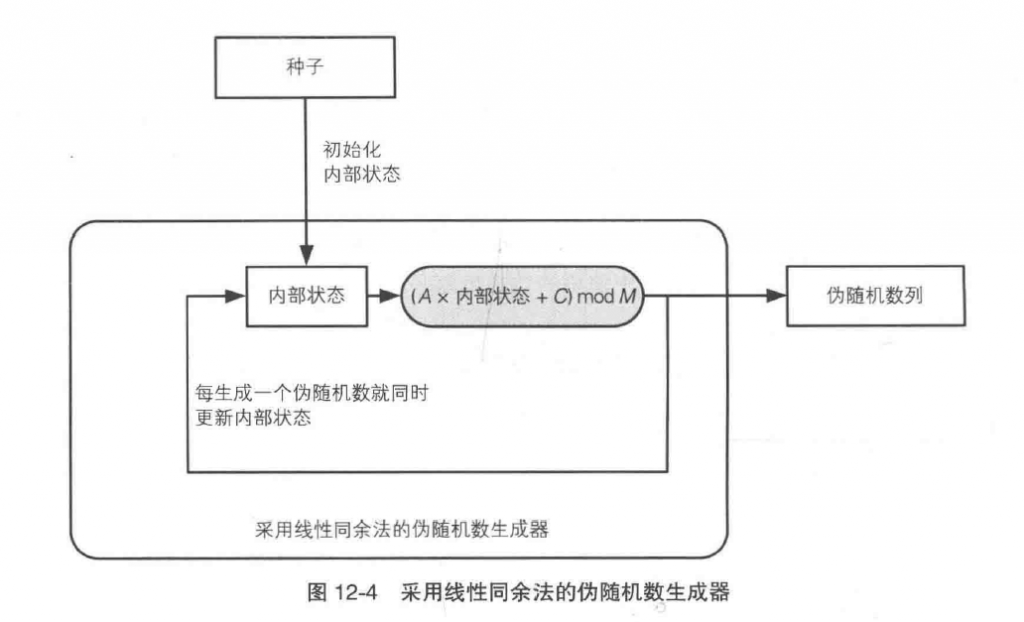
但是在连续的计算后,我们可以发现其拥有周期性,所以不可以用于密码技术。
单项散列函数法
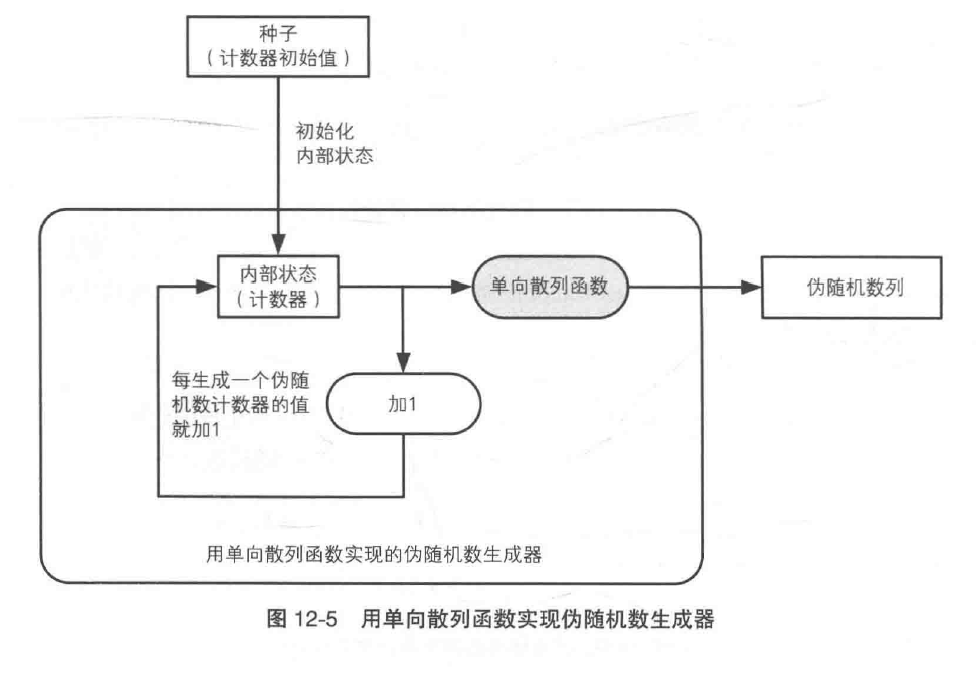
- 用伪随机数的种子初始化内部状态(计数器)
- 用单项散列函数计算计数器的散列值
- 将散列值作为伪随机数输出
- 计数器的值加1
- 根据需要的伪随机数数量重复2~4的步骤
单项散列函数的单向性是支撑伪随机数生成器不可预测性的基础。
密码法
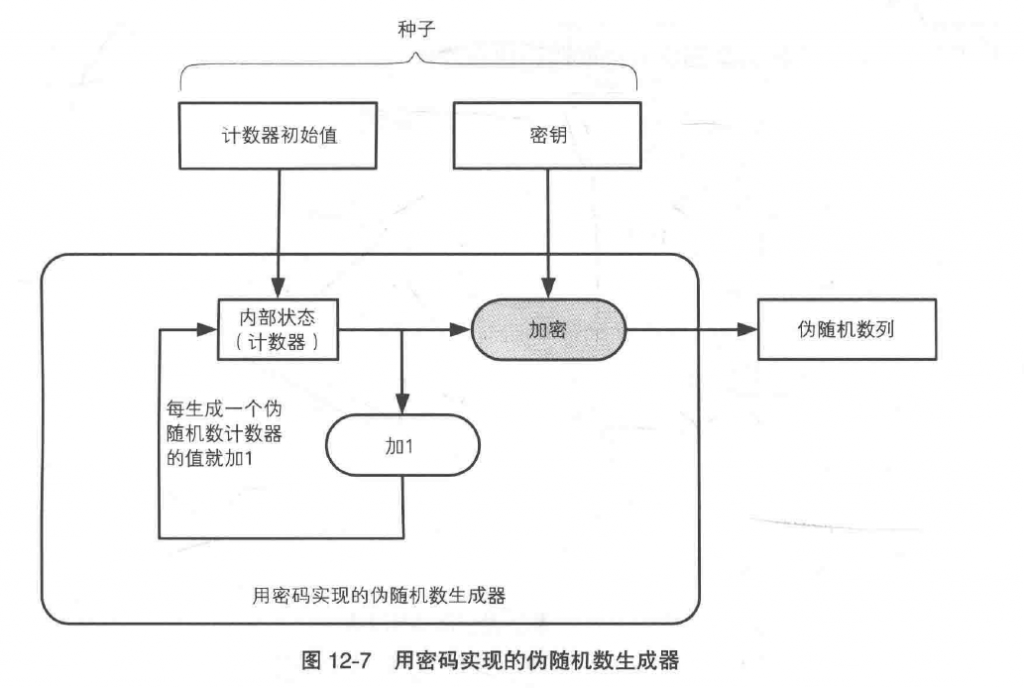
- 初始化内部状态
- 秘钥加密计数器的值
- 将密文作为伪随机数输出
- 计数器的值加1
- 根据需要的伪随机数数量重复2~4的步骤
密码的机密性是支撑伪随机数生成器不可预测的基础。
ANSI X9.17
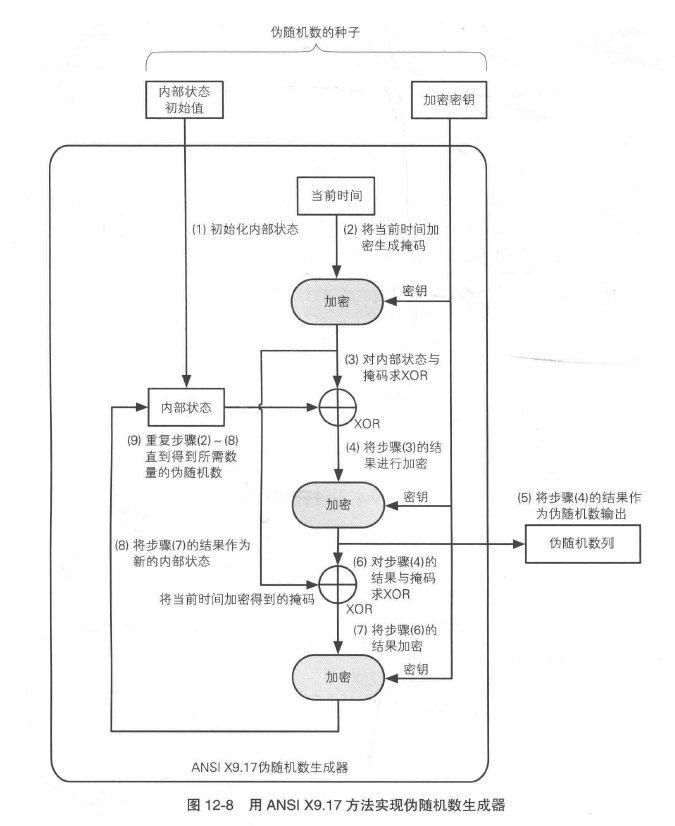
- 初始化内部状态
- 将当前时间加密生成掩码
- 对内部状态与掩码求XOR
- 将步骤3的结果进行加密
- 对步骤4的结果作为伪随机数输出
- 对步骤4的结果与掩码求XOR
- 将步骤6的结果加密
- 将步骤7的结果作为新的内部状态
- 重复步骤2~8直到得到所需数量的伪随机数
对伪随机数生成器的攻击
对种子进行攻击
伪随机数的种子和密码的秘钥同样重要,为了避免种子被直到,我们必须使用具备不可重现性的真随机数作为种子
对随机数池进行攻击
我们一般不会到了需要的时候才当场生成真随机数,而是事先在一个名为随机数池的文件中鸡肋随机比特序列。
随机数池的内容不可以被攻击者知道。

